Lektion G08: Brüche / Bruchrechnung
In dieser Lektion behandeln wir das Rechnen mit Brüchen. Hierzu gibt es eine kurze Einführung ins Thema, danach schauen wir uns an, wie man Brüche addieren, subtrahieren, multiplizieren und dividieren kann - und wie die Regeln zur Bruchrechnung überhaupt entstehen.
Mit der Bruchrechnung erschließen wir übrigens die neue Zahlenmenge der Rationalen Zahlen (Zeichen ℚ). Dies sind alle Zahl, die in einen Bruch umgewandelt werden können. Mehr hierzu in den Videos.
Brüche - Einführung, Erweitern und Kürzen
Eine einfache Einführung: Zähler und Nenner, Erweitern und Kürzen von Brüchen, Zusammenhang zwischen Division und Bruch.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
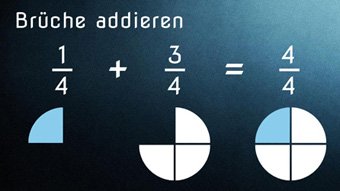
G08-2 Brüche - Addition + SubtraktionAddition und Subtraktion von Brüchen mit gleichen und verschiedenen Nennern, Brüche gleichnamig machen (gemeinsamen Nenner bilden).
-
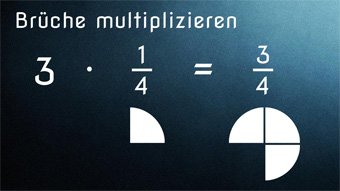
G08-3 Brüche - MultiplikationMultiplikation von Zahl mal Bruch sowie Bruch mal Bruch. Umwandlung einer Zahl in einen Bruch, Herleitung der Multiplikationsregeln für Brüche, Veranschaulichung der einzelnen Rechenschritte.
-
G08-4 Brüche - DivisionDivision von Brüchen inklusive Herleitung der Regeln, Kehrwert/Reziproke, Doppelbruch, Zusammenfassung Bruchrechenregeln. Am Videobeginn: Rechentrick Diagonalkürzen bei Multiplikation.
-
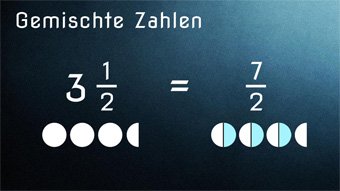
G08-5 Brüche - Brucharten + Gemischte ZahlenStammbruch, echter und unechter Bruch, Scheinbruch, Dezimalbruch (Dezimalzahl), Rechnen mit Gemischten Zahlen, Umwandlung Bruch ↔ Gemischte Zahl, Zahlenmenge: Rationale Zahlen, Vorzeichen bei Zähler und Nenner.
-
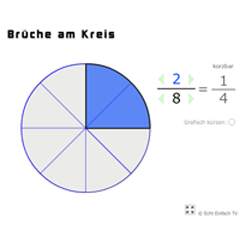 Brüche am KreisStellt Zähler und Nenner des Bruches ein und erkennt die Anteile am Kreis. Falls der Bruch kürzbar ist, wird dies angezeigt.
Brüche am KreisStellt Zähler und Nenner des Bruches ein und erkennt die Anteile am Kreis. Falls der Bruch kürzbar ist, wird dies angezeigt. -
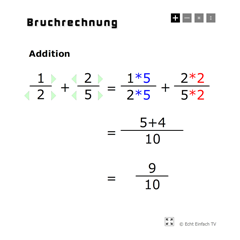 Bruchrechnung (Grundrechenarten)Die vier Grundrechenarten bei beliebigen Brüchen mit Rechenweg, inklusive Erweitern und Kürzen.
Bruchrechnung (Grundrechenarten)Die vier Grundrechenarten bei beliebigen Brüchen mit Rechenweg, inklusive Erweitern und Kürzen. -
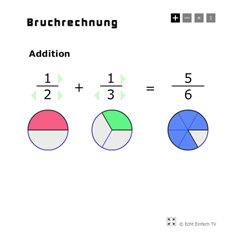 Bruchrechnung (als Flächen)Mit diesem Programm könnt ihr beliebige Brüche berechnen, die gleichzeitig als Flächen angezeigt werden.
Bruchrechnung (als Flächen)Mit diesem Programm könnt ihr beliebige Brüche berechnen, die gleichzeitig als Flächen angezeigt werden. -
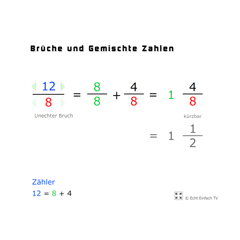 Brüche und Gemischte ZahlenEin unechter Bruch kann in eine Gemischte Zahl umgewandelt werden. Die gemischte Zahl besteht aus einer Ganzen Zahl und einem Restbruch.
Brüche und Gemischte ZahlenEin unechter Bruch kann in eine Gemischte Zahl umgewandelt werden. Die gemischte Zahl besteht aus einer Ganzen Zahl und einem Restbruch. -
 Spiel: Brüche QuizZeigt in diesem Brüche-Spiel, dass ihr die Bruchrechnung beherrscht. In nur 3 Minuten müsst ihr so viele Aufgaben wie möglich richtig berechnen!
Spiel: Brüche QuizZeigt in diesem Brüche-Spiel, dass ihr die Bruchrechnung beherrscht. In nur 3 Minuten müsst ihr so viele Aufgaben wie möglich richtig berechnen! -
 Brüche erweiternBruchrechner zum Lösen von Aufgaben mit Brüchen. Gib Zähler, Nenner und die Erweiterungszahl ein. Ergebnis und Rechenweg werden angezeigt.
Brüche erweiternBruchrechner zum Lösen von Aufgaben mit Brüchen. Gib Zähler, Nenner und die Erweiterungszahl ein. Ergebnis und Rechenweg werden angezeigt. -
 Brüche kürzenBruchrechner zum Lösen von Aufgaben mit Brüchen. Gib Zähler und Nenner ein und der Bruch wird sofort vollständig gekürzt, inklusive Rechenweg.
Brüche kürzenBruchrechner zum Lösen von Aufgaben mit Brüchen. Gib Zähler und Nenner ein und der Bruch wird sofort vollständig gekürzt, inklusive Rechenweg.
Hier findest du 80 Arbeitsblätter, mit denen du dein Wissen testen kannst.
-
AB: Lektion Brüche (Teil 1)
-
AB: Lektion Brüche (Teil 2)
-
AB: Lektion Brüche (Teil 3)
-
AB: Lektion Brüche (Teil 4)
-
AB: Lektion Brüche (Teil 5)
-
AB: Lektion Brüche (Teil 6)
-
AB: Lektion Brüche (Teil 7)
-
AB: Lektion Brüche (Teil 8)
-
AB: Lektion Brüche (Teil 9)
-
AB: Erweitern von Brüchen I
-
AB: Erweitern von Brüchen I (Erweitert)
-
AB: Erweitern von Brüchen II
-
AB: Erweitern von Brüchen II (Erweitert)
-
AB: Anteile erkennen mit Brüchen
-
AB: Anteile erkennen mit Brüchen (Erweitert)
-
AB: Brüche am Zahlenstrahl
-
AB: Unechte Brüche am Zahlenstrahl
-
AB: Ungleichnamige Brüche vergleichen
-
AB: Ungleichnamige Brüche vergleichen (Erweitert)
-
AB: Brüche addieren (Teil 1/3)
-
AB: Brüche addieren (Basis) (Teil 2/3)
-
AB: Brüche addieren (Basis) (Teil 3/3)
-
AB: Brüche addieren (Erweitert) (Teil 1/3)
-
AB: Brüche addieren (Erweitert) (Teil 2/3)
-
AB: Brüche addieren (Erweitert) (Teil 3/3)
-
AB: Brüche subtrahieren (Teil 1/3)
-
AB: Brüche subtrahieren (Basis) (Teil 2/3)
-
AB: Brüche subtrahieren (Basis) (Teil 3/3)
-
AB: Brüche subtrahieren (Erweitert) (Teil 1/3)
-
AB: Brüche subtrahieren (Erweitert) (Teil 2/3)
-
AB: Brüche subtrahieren (Erweitert) (Teil 3/3)
-
AB: Brüche mit Zahlen multiplizieren
-
AB: Brüche mit Zahlen multiplizieren (Erweitert)
-
AB: Brüche mit Brüchen multiplizieren (Teil 1/2)
-
AB: Brüche mit Brüchen multiplizieren (Teil 2/2)
-
AB: Brüche mit Brüchen multiplizieren (Erweitert) (Teil 1/2)
-
AB: Brüche mit Brüchen multiplizieren (Erweitert) (Teil 2/2)
-
AB: Brüche durch Zahlen dividieren
-
AB: Brüche durch Brüche dividieren (Teil 1/2)
-
AB: Brüche durch Brüche dividieren (Teil 2/2)
-
AB: Brüche durch Zahlen dividieren (Erweitert)
-
AB: Brüche durch Brüche dividieren (Erweitert) (Teil 1/2)
-
AB: Brüche durch Brüche dividieren (Erweitert) (Teil 2/2)
-
AB: Einheiten mit Brüchen umrechnen I
-
AB: Einheiten mit Brüchen umrechnen I (Erweitert)
-
AB: Einheiten mit Brüchen umrechnen II
-
AB: Einheiten mit Brüchen umrechnen II (Erweitert)
-
AB: Bruchmauern I
-
AB: Bruchmauern I (Erweitert)
-
AB: Bruchmauern II
-
AB: Bruchmauern II (Erweitert)
-
AB: Rechentabelle für Brüche
-
AB: Rechentabelle für Brüche (Erweitert)
-
AB: Brüche und Variablen (Basis)
-
AB: Brüche und Variablen (Erweitert)
-
AB: Sachaufgaben Brüche
-
AB: Sachaufgaben Brüche (Erweitert)
-
AB: Brüche und Dezimalzahlen
-
AB: Kürzen von Brüchen I
-
AB: Kürzen von Brüchen I (Erweitert)
-
AB: Kürzen von Brüchen II
-
AB: Kürzen von Brüchen II (Erweitert)
-
AB: Brüche am Zahlenstrahl (Kürzen)
-
AB: Brüche sinnvoll erweitern
-
AB: Brüche vollständig kürzen
-
AB: Größen mit Brüchen angeben
-
AB: Gemischte Zahlen und Brüche
-
AB: Unechte Brüche vergleichen
-
AB: Begriffe beim Bruch
-
AB: Brüche am Kreis einzeichnen (1)
-
AB: Brüche am Kreis einzeichnen (2)
-
AB: Brüche-Pizza
-
AB: Brüche am Kreis
-
AB: Brüche am Rechteck einzeichnen
-
AB: Stammbrüche zeichnerisch darstellen
-
AB: Geburtstagskuchen aufteilen
-
AB: Stammbrüche erkennen (Teil 1)
-
AB: Stammbrüche erkennen (Teil 2)
-
AB: Stammbrüche erkennen (Teil 3)
-
AB: Gleichnamige Brüche vergleichen
Hier findest du 48 Lernchecks, mit denen du dein Wissen testen kannst.
-
CHECK: Anteile erkennen und mit Brüchen ausdrücken
-
CHECK: Brüche am Kreis ausdrücken
-
CHECK: Brüche als Flächen (Erweitern)
-
CHECK: Brüche als zwei Flächenanteile
-
CHECK: Brüche kürzen I
-
CHECK: Brüche kürzen II
-
CHECK: Brüche erweitern I
-
CHECK: Brüche erweitern II
-
CHECK: Brüche am Zahlenstrahl
-
CHECK: Ungleichnamige Brüche vergleichen
-
CHECK: Zwei Brüche addieren
-
CHECK: Mehrere Brüche addieren
-
CHECK: Zwei Brüche subtrahieren
-
CHECK: Mehrere Brüche subtrahieren
-
CHECK: Zwei Brüche multiplizieren
-
CHECK: Mehrere Brüche multiplizieren
-
CHECK: Zwei Brüche dividieren
-
CHECK: Mehrere Brüche dividieren
-
CHECK: Einheiten umrechnen (Bruch zu Dezimalzahl)
-
CHECK: Einheiten umrechnen (Dezimalzahl zu Bruch)
-
CHECK: Rechentabelle Brüche I
-
CHECK: Rechentabelle Brüche II
-
CHECK: Rechentabelle Brüche III
-
CHECK: Rechentabelle Brüche IV
-
CHECK: Brüche und Variablen (Addition)
-
CHECK: Brüche und Variablen (Subtraktion)
-
CHECK: Begriffe beim Bruch
-
CHECK: Gleichnamige Brüche vergleichen
-
CHECK: Kürzen und Erweitern von Brüchen erklären
-
CHECK: Brüche vollständig kürzen
-
CHECK: Brüche sinnvoll erweitern
-
CHECK: Gemischte Zahlen und Brüche
-
CHECK: Unechte Brüche vergleichen
-
CHECK: Brüche als Flächen darstellen
-
CHECK: Brüche als Flächen (Kürzen)
-
CHECK: Unechte Brüche am Zahlenstrahl
-
CHECK: Größen mit Brüchen (Bruch zu Kommazahl)
-
CHECK: Größen mit Brüchen (Kommazahl zu Bruch)
-
CHECK: Brüche am Zahlenstrahl (Kürzen)
-
CHECK: Bruchmauern I
-
CHECK: Bruchmauern II
-
CHECK: Bruchmauern III
-
CHECK: Bruchmauern IV
-
CHECK: Bruchmauern V
-
CHECK: Gemischte Aufgaben I
-
CHECK: Gemischte Aufgaben II
-
CHECK: Gemischte Aufgaben III
-
CHECK: Gemischte Aufgaben IV
Artikel im Wiki:
- Brüche - Formelübersicht
- Brüche - Einführung
- Brüche am Kreis
- Brüche am Beispiel der Pizza
- Bruchzahlen und Anteile (zeichnerisch)
- Bruchteile zeichnerisch darstellen
- Brüche kürzen
- Brüche erweitern
- Brüche am Zahlenstrahl
- Gleichnamige Brüche
- Ungleichnamige Brüche
- Kehrwert beim Bruch
- Brüche addieren
- Brüche subtrahieren
- Brüche multiplizieren
- Brüche dividieren
- Brüche vollständig kürzen
- Brüche sinnvoll erweitern
- Brucharten
- Doppelbruch
- Anteile mit Brüchen berechnen
- Unechte Brüche
- Unechte Brüche am Zahlenstrahl
- Gemischte Zahlen
- Gemischte Zahl in Bruch umwandeln
- Bruch in gemischte Zahl umwandeln
- Rationale Zahlen („Bruchzahlen“)
- Dezimalzahl zu Bruch umrechnen
- Bruch zu Dezimalzahl umrechnen
- Größen mit Brüchen angeben
- Einheiten mit Brüchen umrechnen
- Dezimalbrüche
- Dezimalbruchentwicklung
- Kehrwert bei einer Gleichung
- Brüche am Computer schreiben
- Denkprozesse beim Bruchrechnen
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.